高中不等式柯西公式经常难倒很多考生。那么高中数学柯西不等式公式是什么？高中数学柯西不等式公式有多难？本期小编将为大家带来柯西不等式的一般形式和推导过程，同时为大家附上柯西不等式6个基本公式和例题，供大家参考。
什么是柯西不等式公式？
柯西不等式，是数学家柯西(Cauchy)在研究数学分析中的“流数”问题时得到的。
从历史的角度讲，柯西不等式应称作Cauchy-Buniakowsky-Schwarz不等式（柯西-布尼亚科夫斯基-施瓦茨不等式），因为正是后两位数学家彼此独立地在积分学中推而广之，才将这一不等式应用到近乎完善的地步。
高中数学柯西不等式公式
柯西不等式高中公式包括：
1、二维形式
此推广形式又称卡尔松不等式，其表述是：在m×n矩阵中，各列元素之和的几何平均不小于各行元素的几何平均之和。二维形式是卡尔松不等式n=2时的特殊情况 。
2、向量形式
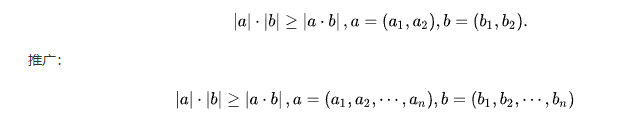
3、三角形式
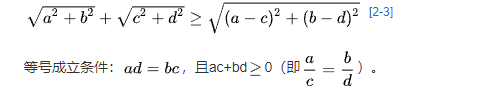
4、概率论形式
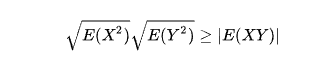
5、积分形式
6、一般形式
柯西不等式验证推导
1、二维形式的证明
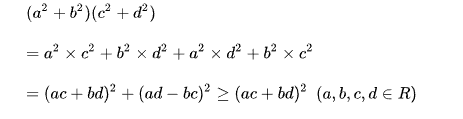
等号在且仅在ad－bc=0即ad=bc时成立。
2、三角形式的证明
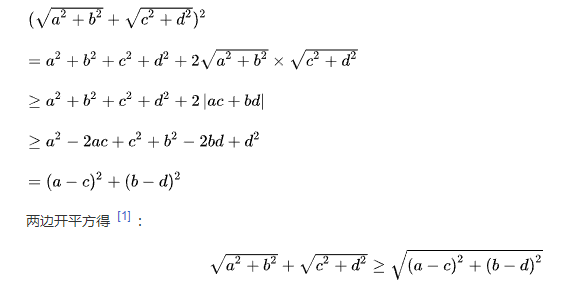
3、向量形式的证明
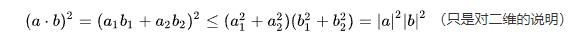
4、概率论形式的证明
5、积分形式的证明
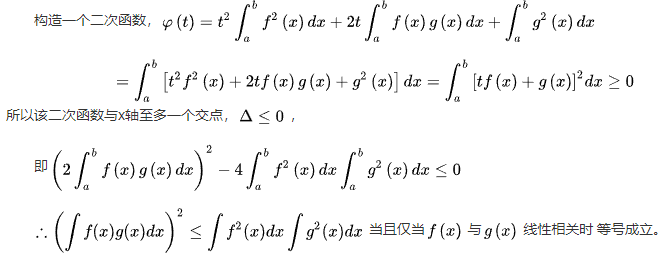
6、一般形式的证明
剩余几种情形都是一般情形的特例，完全可以用一般情形的证明方法来证。
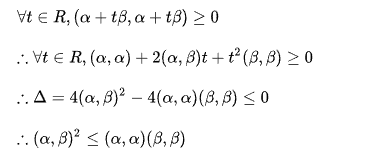
另一种写法：
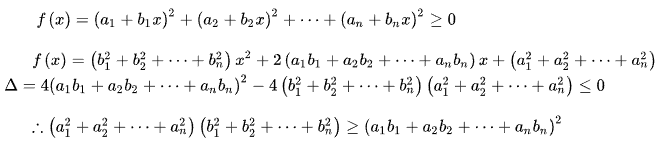
高中数学柯西不等式应用例子
柯西不等式在求某些函数最值中和证明某些不等式时是经常使用的理论根据，技巧以拆常数，凑常值为主。
巧拆常数证不等式
求某些函数最值
