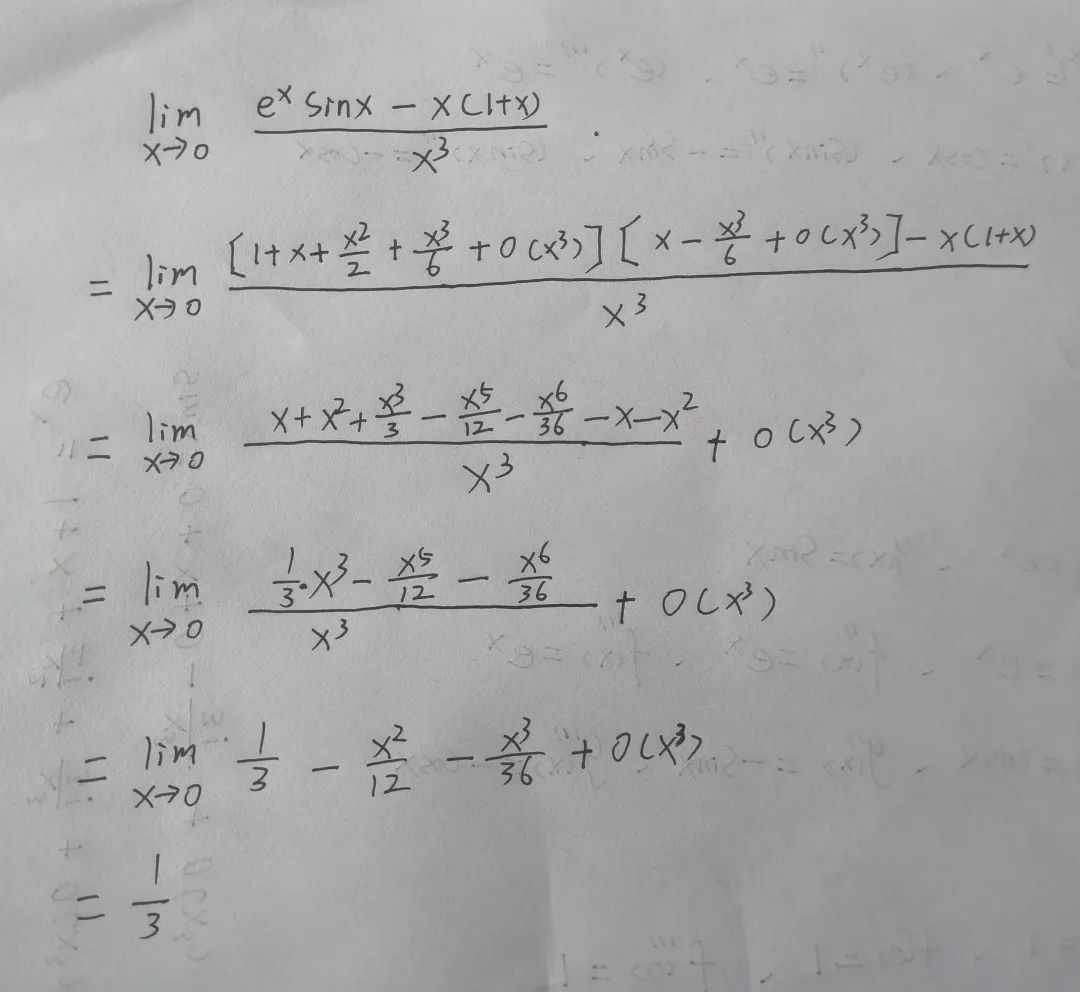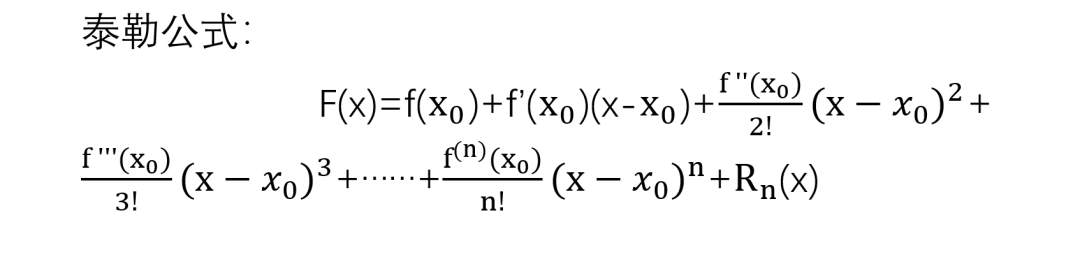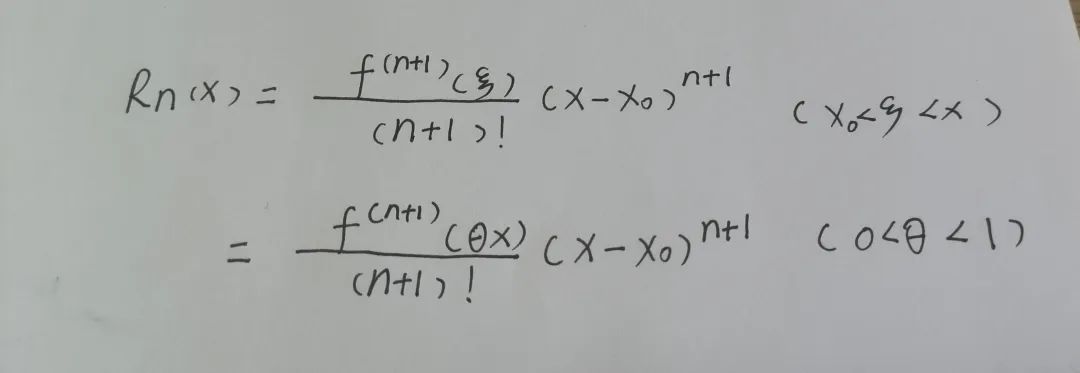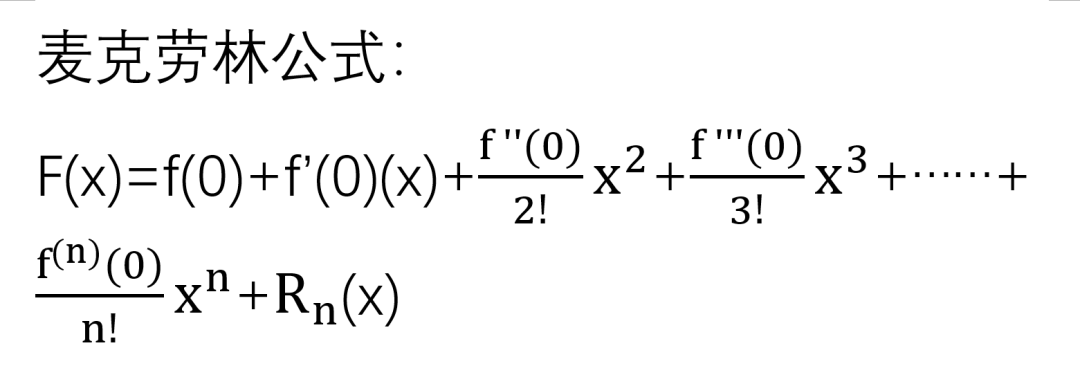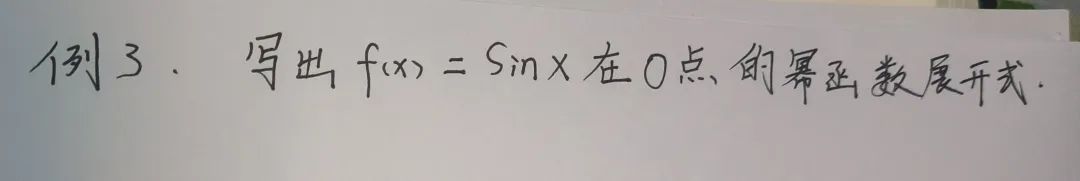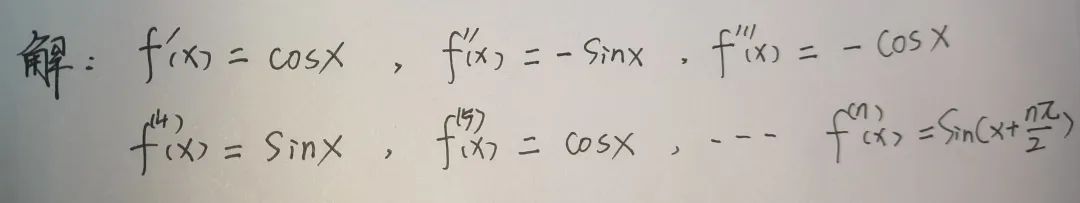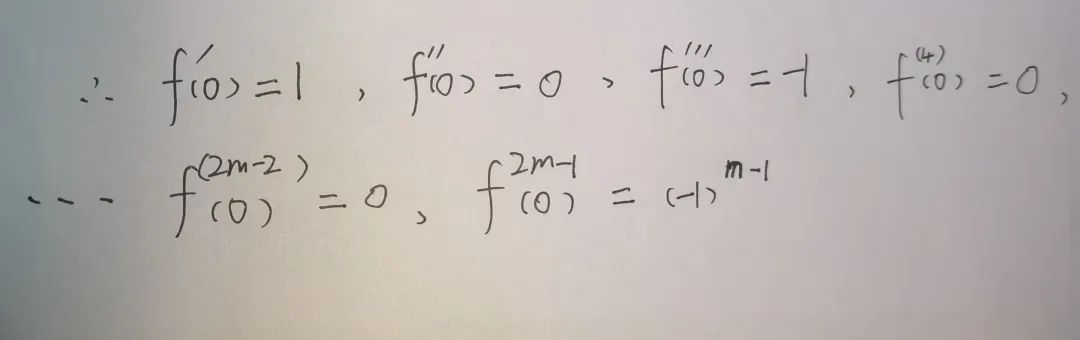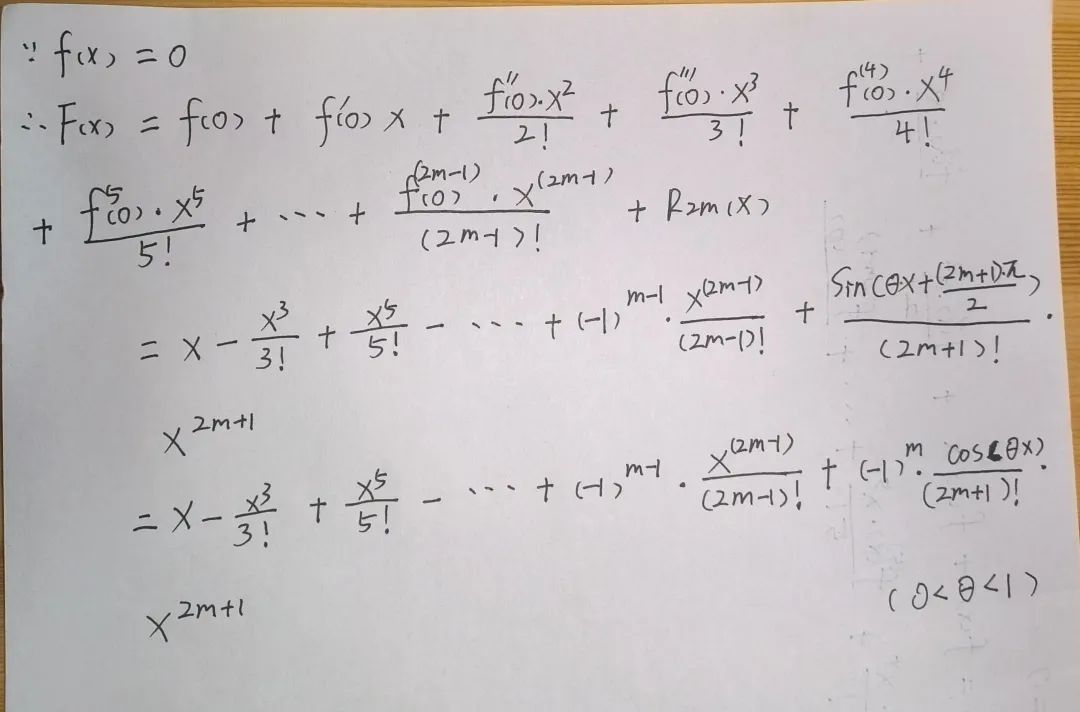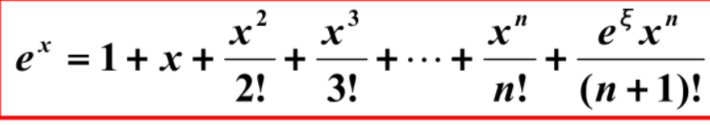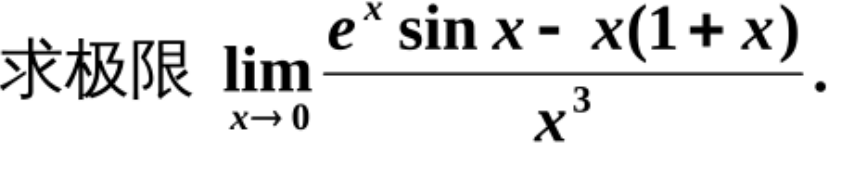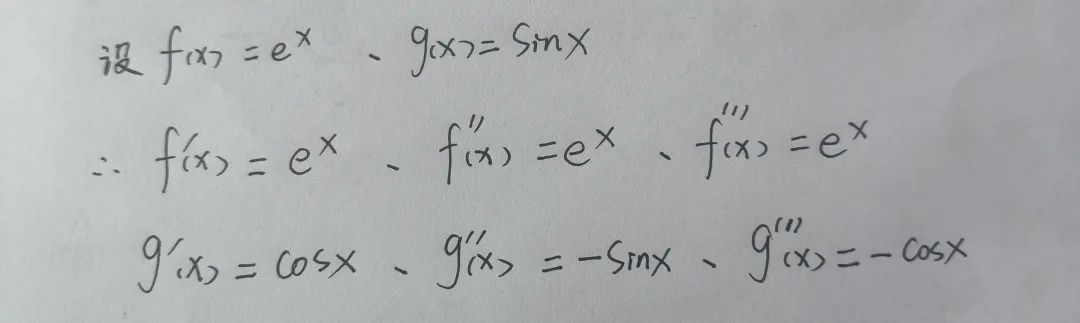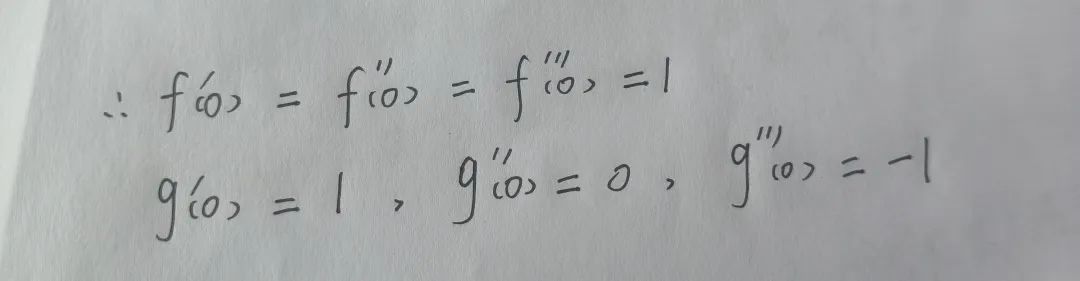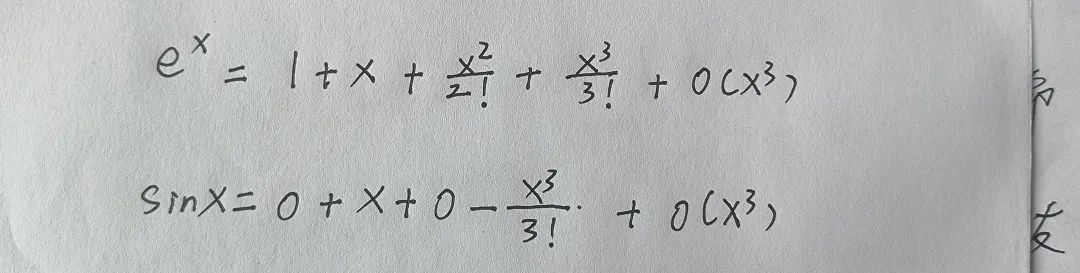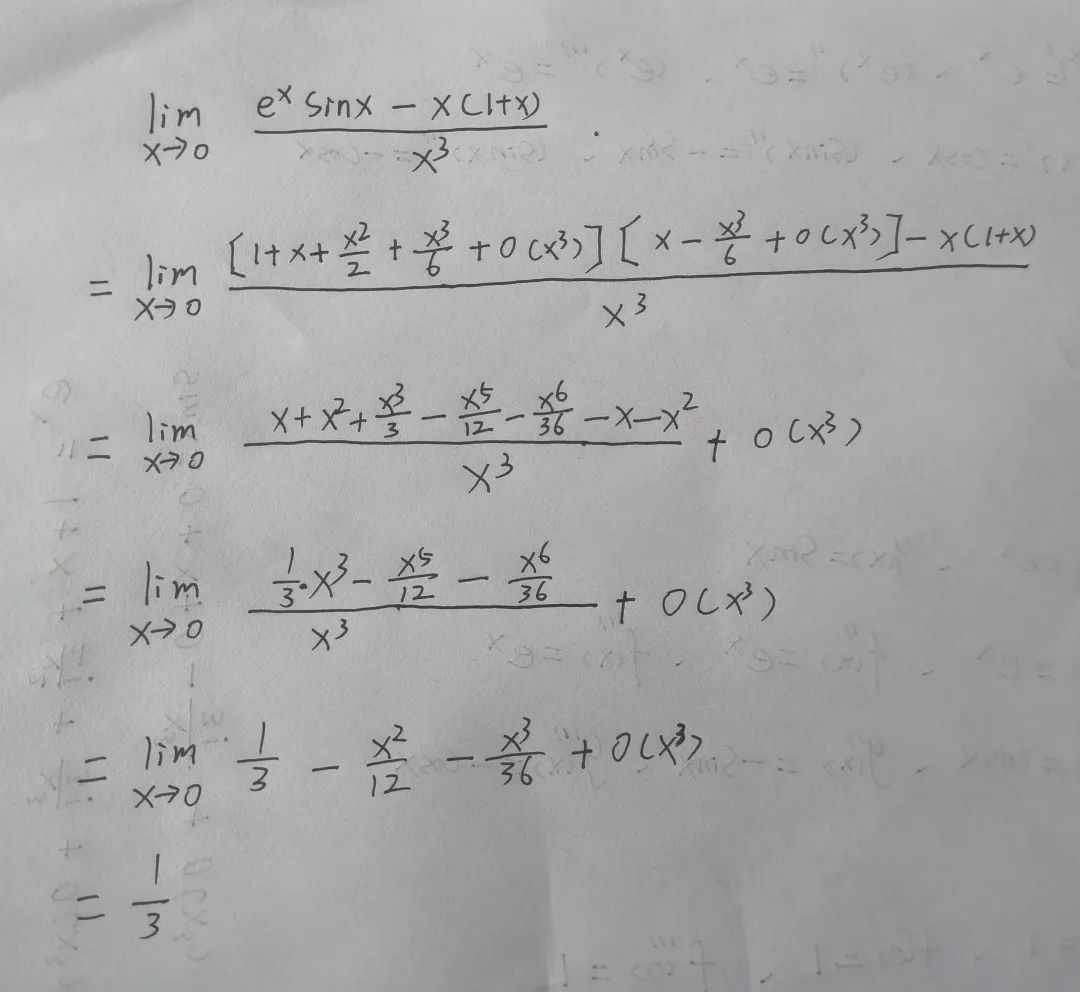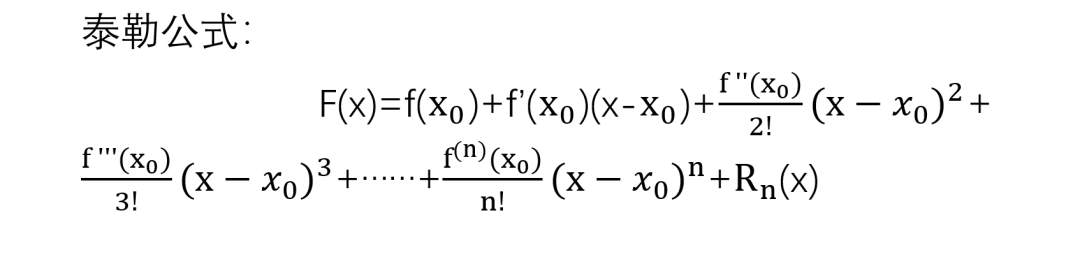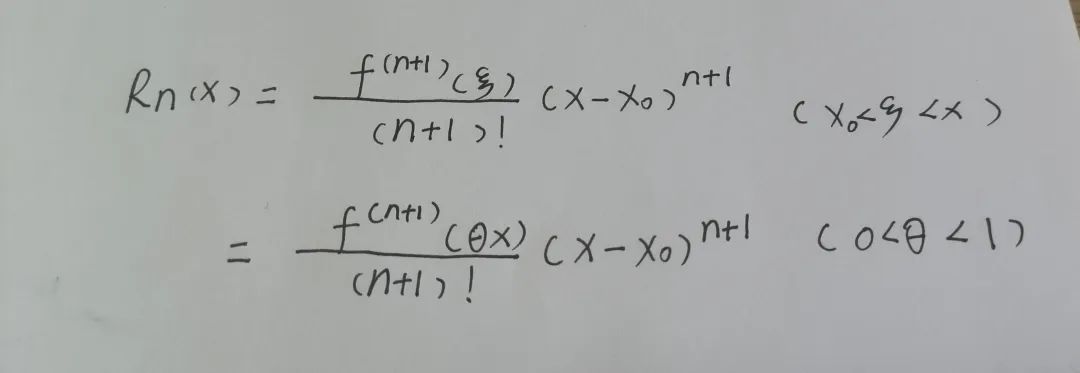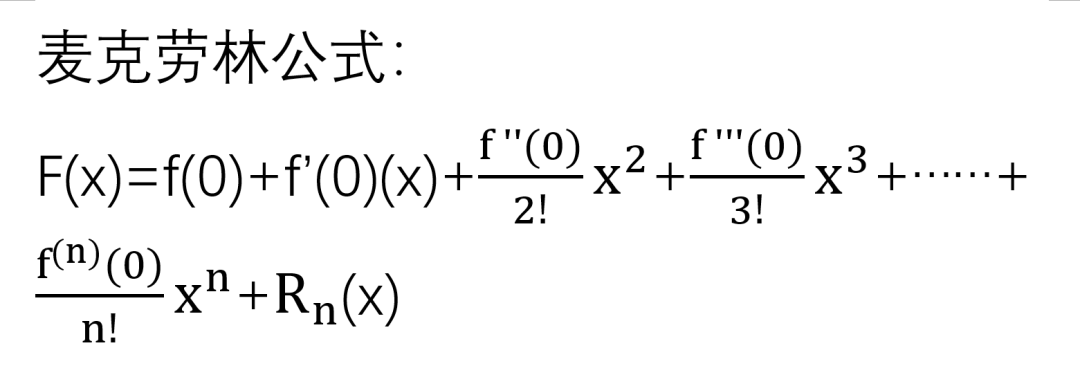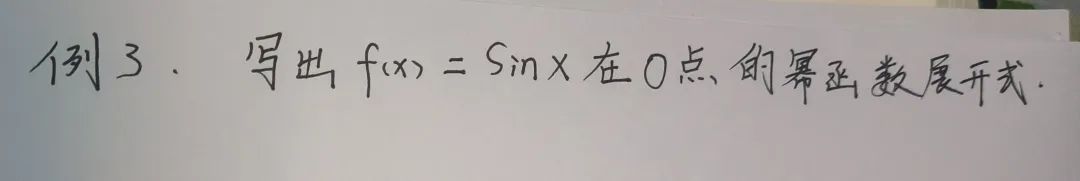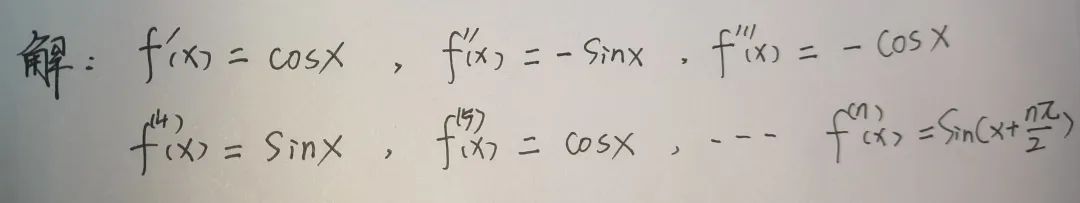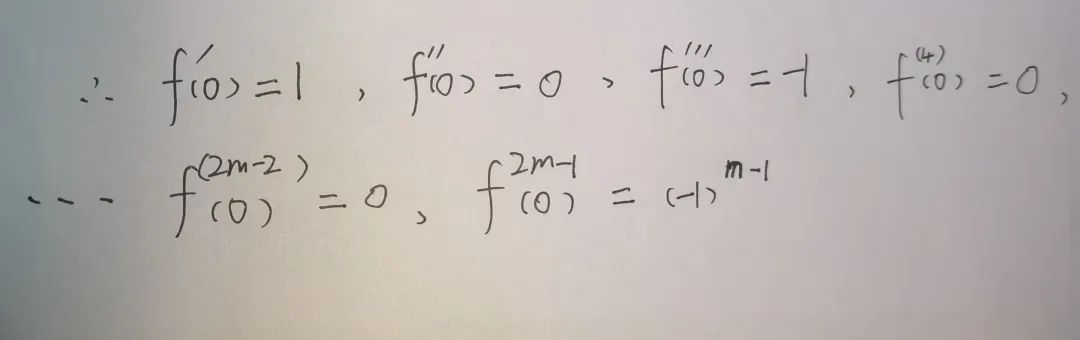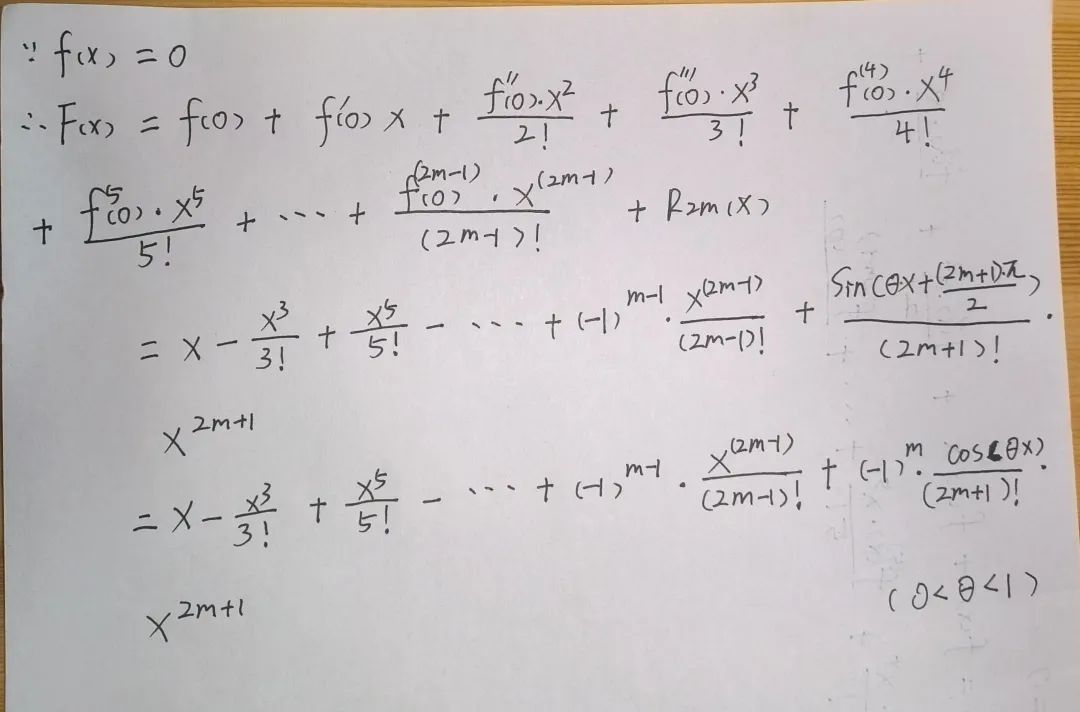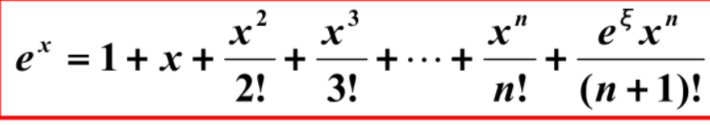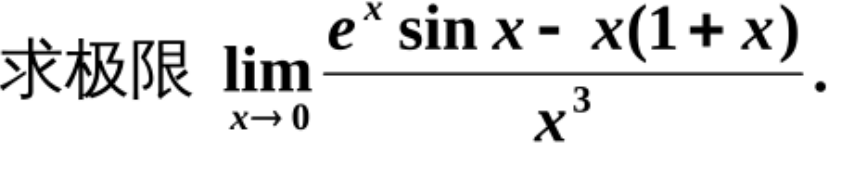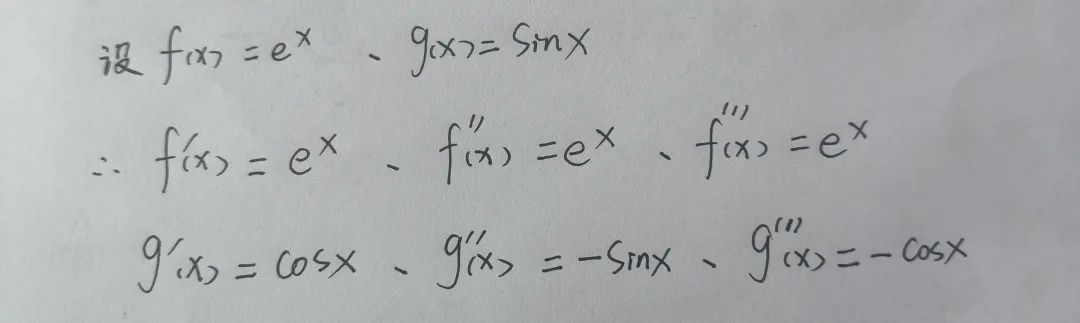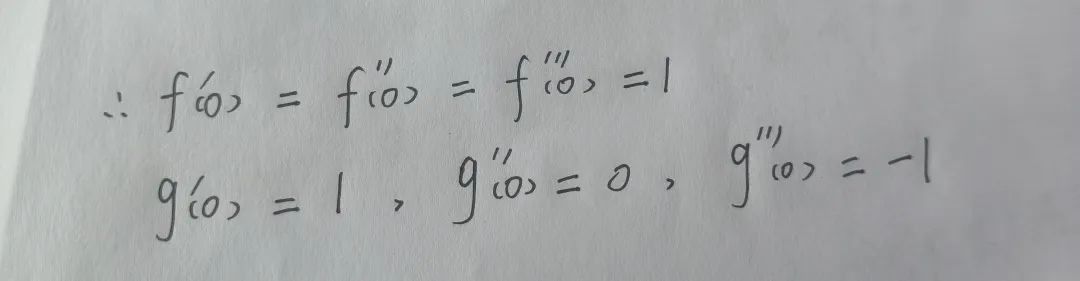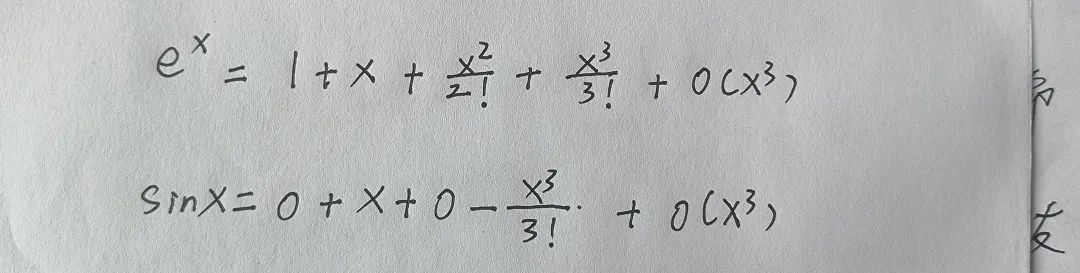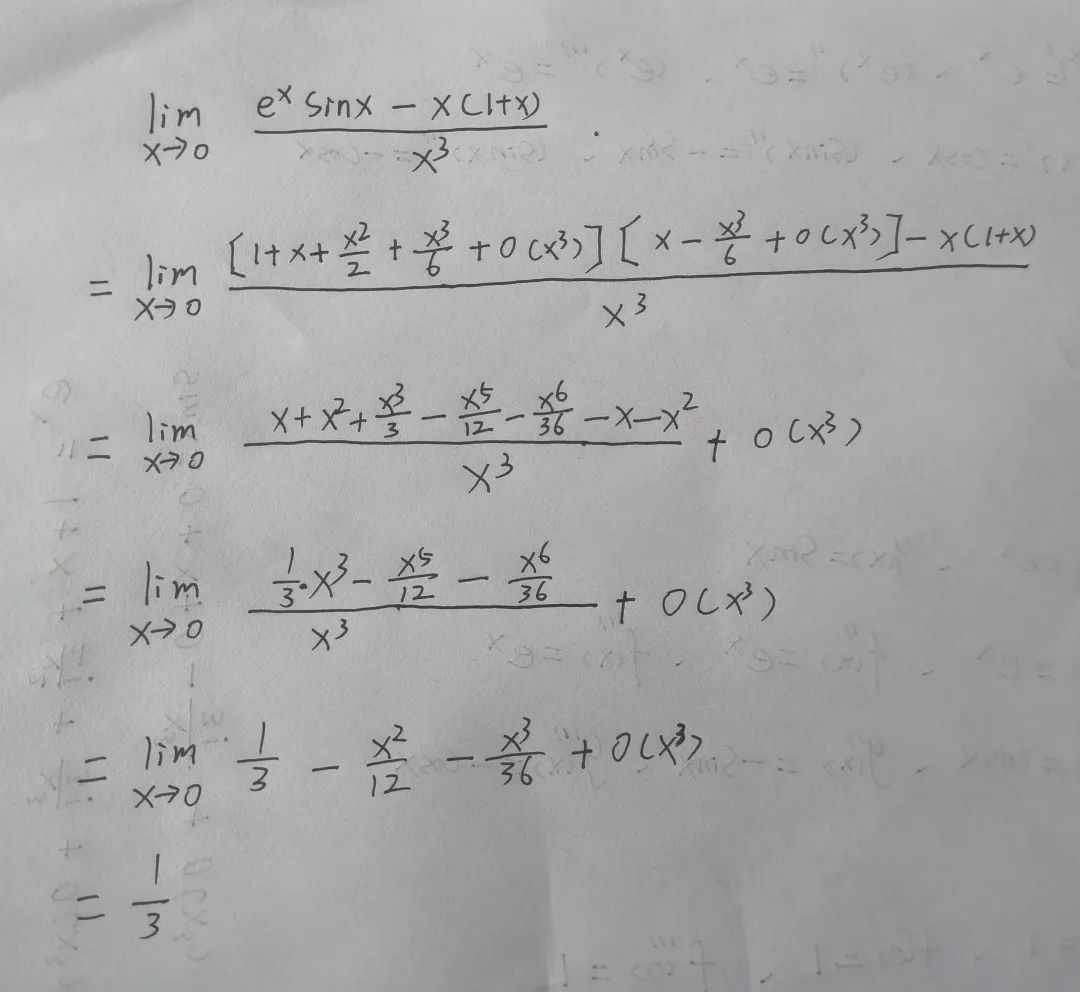1.
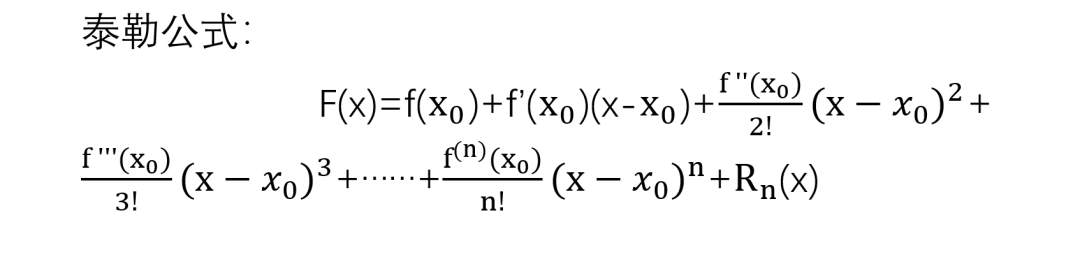
在这里面 Rn(x)叫做拉格朗日余项.
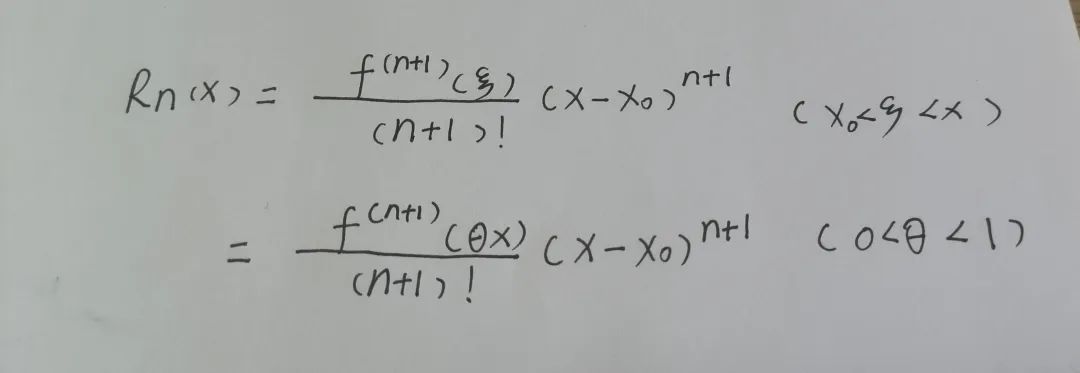
其实这里面泰勒公式的本质就是近似,也就是对于任意一个函数F(x)在x=x0处都可以近似于一个常数乘以幂函数作和来表示,但只要是近似就一定会有误差,泰勒展开项越多,误差就越小,而拉格朗日余项又表示泰勒展开与原式之间的误差,所以误差越小,拉格朗日余项就越趋近于0。2.当F(x)在x=0处展开泰勒公式时得到麦克劳林公式:
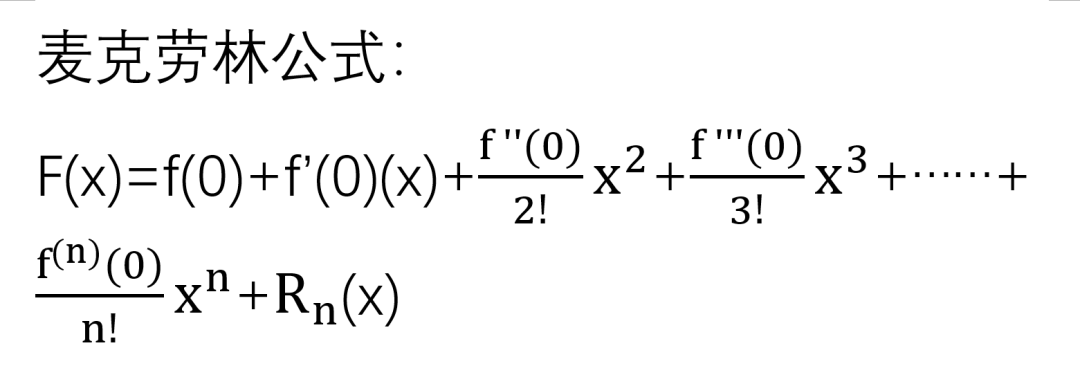
当x→0时,Rn(x)是关于x^n的高阶无穷小,所以当|x|特别特别小的时候,拉格朗日余项又可以表示为:Rn(x)=o(x^n) ,我们把o(x^n)称为佩亚诺余项3.那么到底如何去求一个函数的泰勒展开式呢?我们以题为例: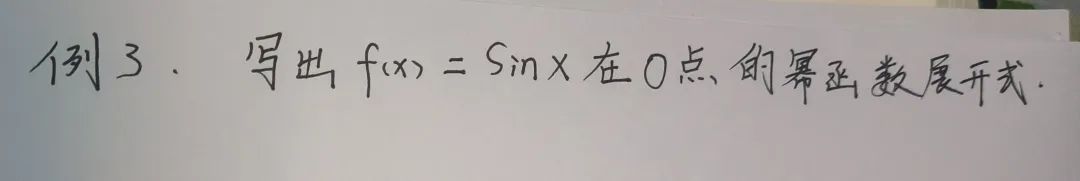
①首先要求出函数的n阶导数.
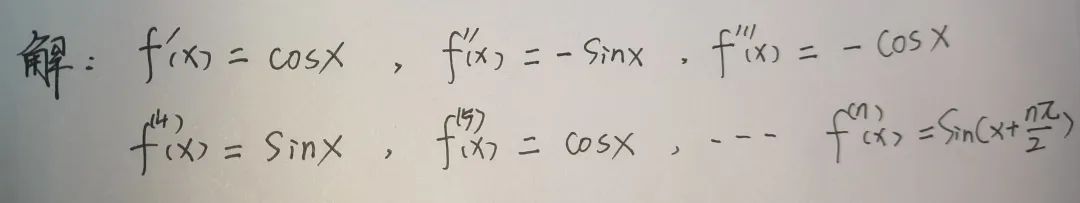
②再把x=0代入进去.
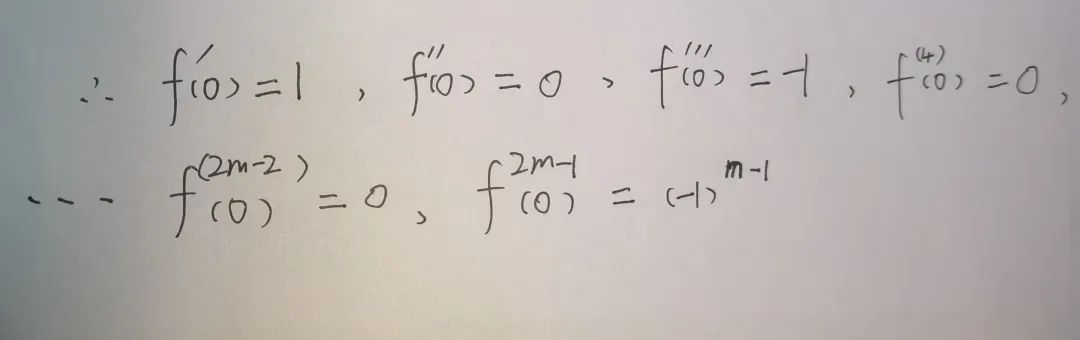
注:不同函数有不同的规律,在这里面当sinx导数为偶次阶导数时,结果都为零。所以只需找出奇次阶导数规律即可,由于正常情况下的最后一个导数是n阶的,无法确定奇偶性,为了体现规律性,我们一般最后一个取到2m+1或2m-1,具体用哪个只要和项数对应起来即可.我这里面是取到2m-1,因为不算f(0)这项的话m=1时正好是第一项,x的幂数也是一又正好对应着一阶导数,分母又正好是1的阶乘.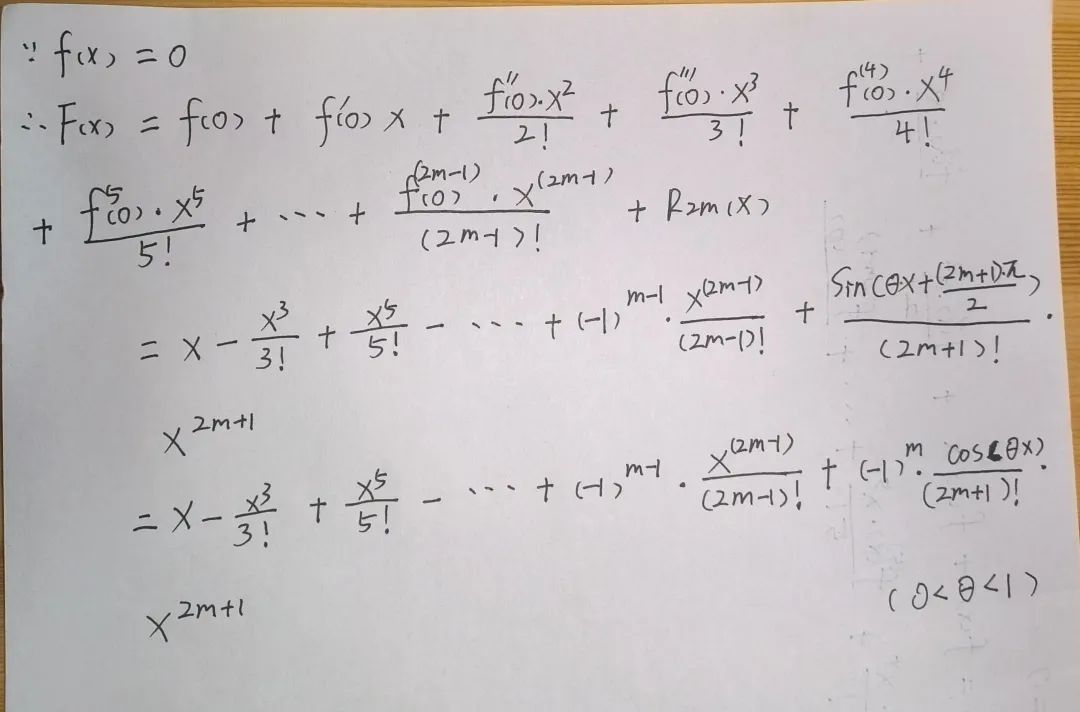
这里面最后sin中的θx看作一个锐角而(2m+1)/2一定是奇数,所以一定能变成cosθx,而系数取前几项即可找出规律.到此一个函数的泰勒展开过程结束


通过观察你会发现,他们各自的前几项不就是我们之前学过的等价无穷小吗?他和泰勒公式展开有什么联系呢?
①等价无穷小相比泰勒公式计算更简单一些,同样是近似于f(x)但相比泰勒公式展开误差会更大一些.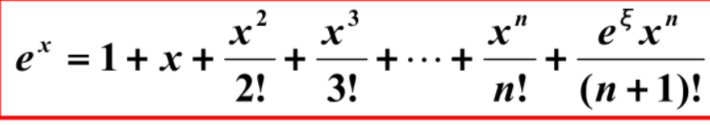
首先要看等号右边,除了1以外都是无穷小,这里面x是最低阶的无穷小,剩下都可以看作高阶无穷小,所以高阶加低阶就等价于低阶,也就是e^x~1+x(前提是x→0)6.利用泰勒公式求极限:(用带佩亚诺余项的泰勒公式)
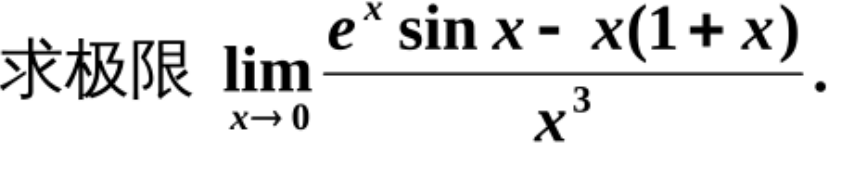
这类题的规律就是,把分子除了幂函数以外的地方分别泰勒展开,看他的分母中x的幂的次数,次数是n就把泰勒展开到第n+1项,因为最前边有一项是f(0)①分别求出e^x和sinx的一到三阶导数
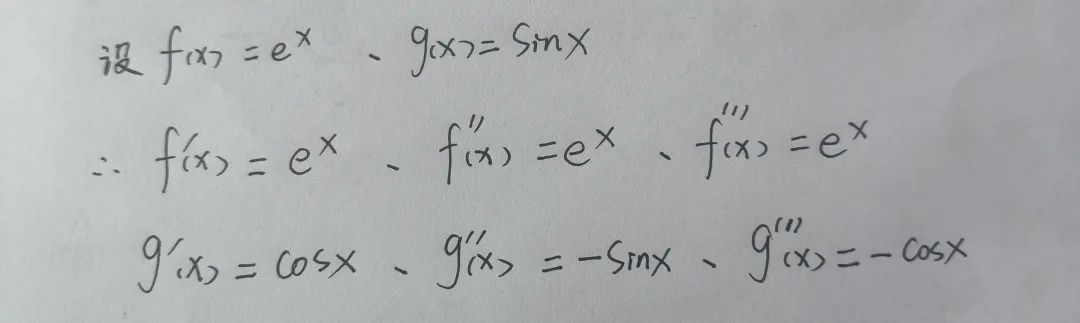
②因为x→0,即在x=0处的泰勒展开,所以把零带入到x中
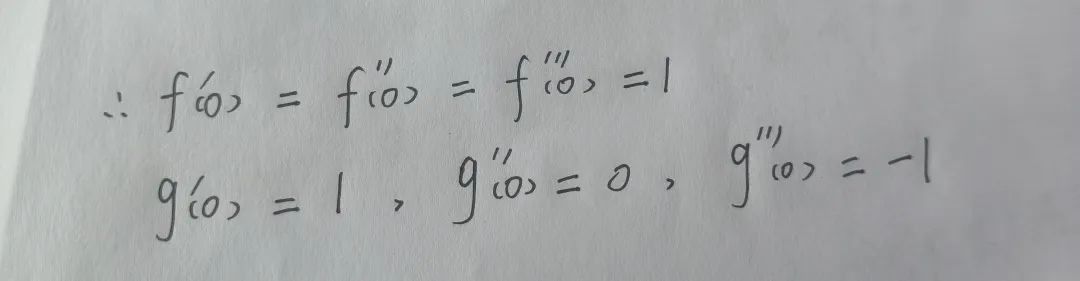
③因为f(0)=1、g(0)=0,所以带有佩亚诺余项的前四项展开式为
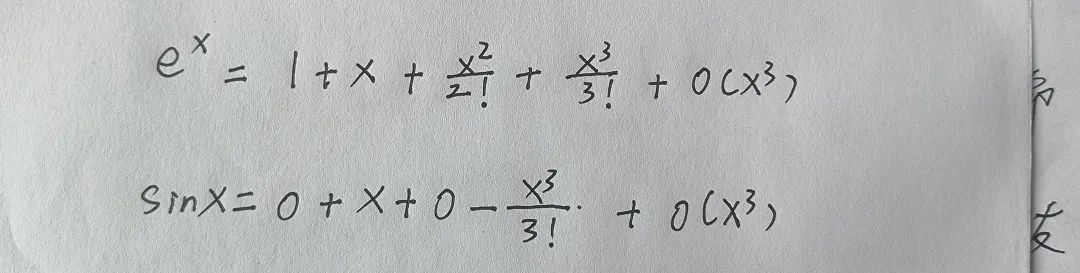
④把他们代入原式中可得